|
Basic Math for Physics
Algebra
If a # is … to a variable, |
then … the # to solve for the variable |
Example |
Added |
Subtract |
5 = x + 2
-2 -2
5-2 = x |
Subtracted |
Add |
3 = x – 6
+6 +6
3-6 = x |
Multiplied |
Divide |
2 = 4x
2/4 4x/4
2/4 = x |
Divided |
Multiply |
2 · 6 = x · 2
2
2 · 6 = x |
Calculations with Significant Figures
Adding & Subtracting:
- Perform the calculation
- Determine the least # of decimal places in problem
- Round answer to that # of decimal places
- Example: 10.027 g ® 3 decimal places
- - 1.5 g ® 1 decimal place
- 8.527 g ® 8.5 g (1 decimal place)
-
Multiplying & Dividing:
- Perform the calculation
- Determine the least # of sig figures in problem
- Round answer to that # of sig figures
- Example: 10.027 g ® 5 sig figs
- 1.50 mL ® 3 sig figs
- answer = 6.6847 g/mL ® 6.68 g/mL (3 sig digs)
Scientific Notation
- Scientific Notation—a short hand method of writing numbers using powers of 10.
-
- Writing scientific notation:
- The decimal point is always moved to after the 1st non-zero number.
- Count the number of times the decimal point is moved and use this as the power of 10.
- “Big” numbers (>1) have positive exponents. “Small” numbers (<1) have negative exponents.
- Examples: 1027500.456 ® 1.027500456 ´ 106
- 0.0007543 ® 7.543 ´ 104
-
- Reading scientific notation:
- Power of 10 = number of times to move decimal point
- Positive powers = make the number “Big” (>1). Negative exponents = make the number “Small” (<1)
- Examples: 3.25 ´ 10-6 ® 0.00000325
- 7.2004 ´ 104 ® 7200.4
Math with Exponents
- Calculations with exponents:
Anything to the power of “1” = itself
Anything to the power of “0” = 1
Multiplying (with the same base) à add the powers
Dividing (with the same base) à subtract the powers
When taking a power of a power à multiply the powers
A negative power puts the number on the opposite side of the fraction & the power becomes positive.
- 3-2 = 1/32
-
- Calculations with scientific notation
Adding (with same power of 10): Add numbers and keep power of 10
- 2 ´ 103 + 3 ´ 103 = 5 ´ 103
Subtracting (with same power of 10): Subtract numbers and keep power of 10
- 3 ´ 103 – 3 ´ 103 = -1 ´ 103
Multiplying: Multiply numbers & add powers of ten
- 2 ´ 106 · 3 ´ 103 = 6 ´ 1018
Dividing: Divide numbers & subtract powers of 10
- 2 ´ 106 ¸ 3 ´ 103 = 0.67 ´ 103
Taking it to a power: Take the number to the power and multiply the power of 10 by the power
Roots: Take the number to the root and divide the power of 10 by the root
Trig functions
Quadratic Equation
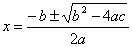 where where 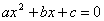
Example: If 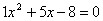
Then 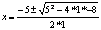
Calculator Survival
- Always use the ¸ key to designate a number is on the bottom of an expression.
- Always use the EE (or EXP) key to enter scientific notation.
- Always use parenthesis around addition or subtraction when combining it with other operations
- To make something negative (when taking the number to a power), keep the negative outside of the parenthesis.
|