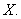Function (from a set X to a set Y):
A correspondence that associates with each element x (independent variable) of X and a unique element y (dependent variable) of Y. Notation: 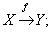
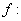
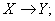 or
or 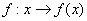 .
.
Domain of a function:
The data set of all real numbers for which the correspondence makes sense.
One to one functions:
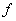 is a function from
is a function from 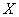 to
to 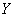 .
.
Increasing functions:
If S is a subset of X and 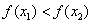 whenever
whenever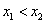 , in S, then
, in S, then 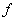 is an increasing function in S.
is an increasing function in S.
Decreasing functions:
If S is subset of X and 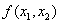 whenever
whenever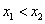 , in S, then
, in S, then 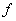 is a decreasing function in S.
is a decreasing function in S.
Slope:
If 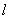 is a line which is not parallel to the
is a line which is not parallel to the 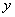 -axis and if
-axis and if 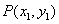 and
and 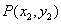 are distinct points on
are distinct points on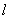 , then the slope
, then the slope 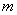 of
of 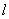 is given by:
is given by:
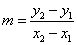 .
.
Equation of a curve:
Suppose of a curve composed of points whose coordinates are 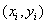 for
for 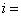 1, 2,….
1, 2,….
If there is an equation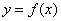 , by which all the
, by which all the 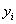 can be calculated through substituting
can be calculated through substituting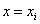 , the equation
, the equation 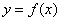 is called the equation of the curve.
is called the equation of the curve.
Equation of a line:
If the slope of a line is given (denoted by 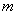 ) and if a point on the line is given (coordinate is
) and if a point on the line is given (coordinate is 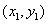 ) , the line equation would be
) , the line equation would be 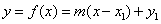 .
.
Vertical shifts:
If 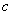 is a real number, the graph of
is a real number, the graph of 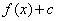 is the graph of
is the graph of 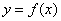 shifted upward
shifted upward 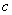 units for
units for 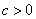 or shifted downward for
or shifted downward for 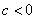 .
.
Horizontal shifts:
If 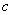 is a real number, the graph of
is a real number, the graph of 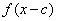 is the graph of
is the graph of 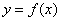 shifted to the right
shifted to the right 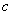 units for
units for 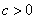 or shifted to the left
or shifted to the left 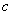 units for
units for 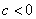 .
.
Reflection in the y-axis:
The graph of the function 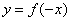 is the graph of
is the graph of 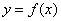 reflected in the y-axis.
reflected in the y-axis.
Reflection in the x-axis:
The graph of the function 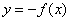 is the graph of
is the graph of 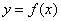 reflected in the x-axis.
reflected in the x-axis.
Vertical stretching and shrinking:
If 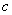 is a real number, the graph of
is a real number, the graph of  is the graph of
is the graph of 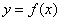 stretched vertically by
stretched vertically by 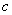 for
for 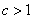 or shrunk vertically by
or shrunk vertically by 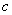 for
for 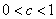 .
.
Horizontal stretching and shrinking:
If 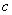 is a real number, the graph of
is a real number, the graph of 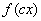 is the graph of
is the graph of 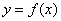 stretched horizontally by
stretched horizontally by 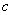 for
for 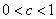 or shrunk horizontally by
or shrunk horizontally by 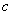 for
for 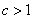 .
.
Composite functions:
If 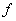 is a function from
is a function from 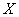 to
to 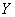 and
and 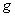 is the function from
is the function from 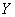 to
to 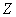 , then the composite function
, then the composite function 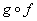 is the function from
is the function from  to
to 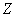 defined by
defined by 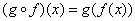 .
.
Inverse functions:
Let 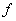 be a one to one function from
be a one to one function from 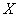 to
to 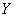 . Then, a function
. Then, a function 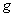 from
from 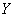 to
to 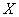 is called the inverse function of
is called the inverse function of 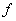 if
if 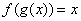 for all
for all 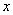 in
in 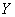 and
and 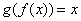 for all
for all 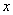 in
in